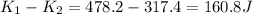Question

A 7.5-kg otter slides down a hill, starting from rest at the top. The sloping surface of the hill is 8.8 m long, and the top is 6.5 m above the base. g no friction, what should the otter's speed be at the bottom? b. If the speed of the otter at the bottom of the hil is 9.2 m/s, how much energy was lost to nonconservative forces on the hill?

Answer 1

Part a)

v = 11.3 m/s

Part b)

Energy loss = 160.8 J

Step-by-step explanation:

Part a)

By Energy conservation we can say that the total energy of the otter at the top of the hill must be same as the total energy of the otter at the bottom of the hill

So we will have

`mgH = (1)/(2)mv^2`

`v = √(2gH)`

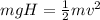
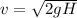
here we know that

H = 6.5 m

now we have

`v = √(2(9.81)(6.5)) = 11.3 m/s`

Part b)

If there is no energy loss then the final speed of the otter at the bottom is given as 11.3 m/s

so final kinetic energy is

`K_1 = (1)/(2)(7.5)(11.3)^2 = 478.2 J`

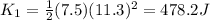
while if it has some conservative force then the final speed will be 9.2 m/s

so final kinetic energy will be

`K_2 = (1)/(2)(7.5)(9.2)^2 = 317.4 J`

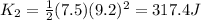
now the energy loss is given as

`K_1 - K_2 = 478.2 - 317.4 = 160.8 J`