Question

Wien's law describes the wavelength of maximum intensity λ max for a blackbody at a particular temperature T: Wien's Law: λ max ⋅ T = 2.90 × 10 − 3 m ⋅ K If we measure the temperature of a blackbody to be about 300 K (a typical air temperature in Florida), at what wavelength would this blackbody's intensity have its maximum, and where in the electromagnetic spectrum is this wavelength?

Answer 1

Step-by-step explanation:

The mathematical expression for Wein's law is given by :

`\lambda_(max).T=2.9* 10^(-3)\ m.K`

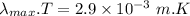
Where

T is the temperature

`\lambda_(max)` is the wavelength

At T = 300 K

`\lambda_(max)=(2.9* 10^(-3)\ m.K)/(T)`

`\lambda_(max)=(2.9* 10^(-3)\ m.K)/(300\ K)`

`\lambda_(max)=0.00000966\ m`

`\lambda_(max)=9.7* 10^(-6)\ m`

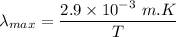
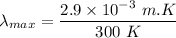
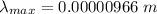
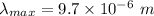
So, the wavelength of black body is
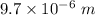`9.7* 10^(-6)\ m` and this wavelength lies in infrared region of the spectrum. Hence, this is the required solution.