Consider a 1 cd isotropic illuminance light source. Answer the following: a.What is luminance of light 10 ft from the source? b. How much total light falls on a 1 str patch that…

Question

asked May 26, 2020 72.5k views

1 Answer

Rikon · Answer 1 · 2020-06-02T04:20:41+0000

Answer:

The luminance of light and the amount of light are
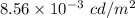$8.56*10^(-3)\ cd/m^2$ and
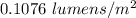$0.1076\ lumens/m^2$ .

Step-by-step explanation:

Given that,

Illuminance of light = 1 cd

Solid angle = 1 str

(a). We need to calculate the luminance

The luminance is the luminance intensity per unit area

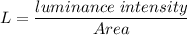
$L=(luminance\ intensity)/(Area)$

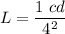
$L=(1\ cd)/(4\pr^2)$

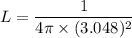
$L=(1)/(4\pi*(3.048)^2)$

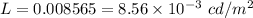
$L=0.008565=8.56*10^(-3)\ cd/m^2$

(b). We need to calculate the amount of the light

Using formula of luminous flux

The luminous flux is equal to the product of the luminance intensity and solid angle.

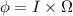
$\phi=I*\Omega$

Where,
$\Omega$ =solid angle

I = luminance intensity

Put the value into the formula

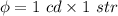
$\phi=1\ cd*1\ str$

The area of a patch on a sphere which is substand by a solid angle
$\Omega$

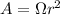
$A=\Omega r^2$

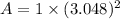
A=1*(3.048)^2

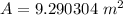
$A=9.290304\ m^2$

We need to calculate the amount of light received by the surface

$B=(\phi)/(A)$

Where,
$\phi$ = luminous flux

A= area

Put the value into the formula

B=(1)/(9.290304)

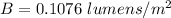
$B=0.1076\ lumens/m^2$

Hence, The luminance of light and the amount of light are
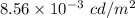$8.56*10^(-3)\ cd/m^2$ and
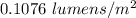$0.1076\ lumens/m^2$ .