Answer:
The tunnel probability for 0.5 nm and 1.00 nm are
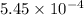 and
and
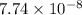 respectively.
respectively.
Step-by-step explanation:
Given that,
Energy E = 2 eV
Barrier V₀= 5.0 eV
Width = 1.00 nm
We need to calculate the value of
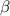
Using formula of
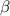
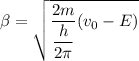
Put the value into the formula
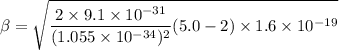
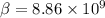
(a). We need to calculate the tunnel probability for width 0.5 nm
Using formula of tunnel barrier
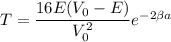
Put the value into the formula
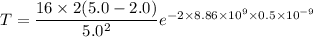
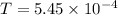
(b). We need to calculate the tunnel probability for width 1.00 nm
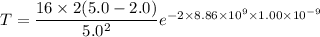
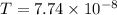
Hence, The tunnel probability for 0.5 nm and 1.00 nm are
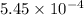 and
and
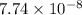 respectively.
respectively.