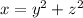Question

Identify and trace the conicoid y2 + z2 = x. Describe its sections by the planes x = 0,y = 0 and z = 0.

Answer 1

`x=y^2+z^2` is a paraboloid with vertex at (0, 0, 0) opening away from the origin centered on the line
`y=z=0`.

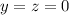When
`x=0`,
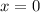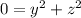`0=y^2+z^2` which means
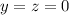`y=z=0`, so that this section is a single point, (0, 0, 0).

When
`y=0`,
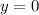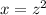`x=z^2` which is a parabola in the
`x`-
`z` plane with vertex at (0, 0, 0).

When
`z=0`,
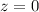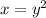`x=y^2` and this section is the same as the previous one, but lying in the the
`x`-
`y`.