Answer:
a)
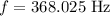
b)
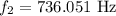
Step-by-step explanation:
Given:
The distance between two speakers (d) = 0.932 m
The distance of the microphone from the midpoint = 2.83 m
Thus, distance of microphone from the nearest speaker (L) = 2.83 - (0.932/2) = 2.364 m
also, the distance of the microphone from the farther speaker (L') = 2.83 + (0.932/2) = 3.296 m
Now,
The path difference is calculated as
L' - L = d = 0.932 m
Now,for a maxima to be produced at the microphone, the waves must constructively interfere.
for this to happen the path difference should be integral multiple of the wavelength.
thus,
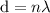
hence, the largest wavelength will be for n = 1,
therefore,
0.932 = 1 × λ
or
λ = 0.932 m
now, the velocity of sound is given as c = 343 m/s
thus, the frequency will be
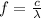
on substituting the values, we get

now, the 2nd largest wavelength will be for n = 2
0.932 = 2 × λ
or
λ = 0.466
thus, the frequency will be
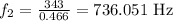
hence, these are the lowest first two frequencies.