Question

The position of an object that is oscillating on an ideal spring is given by the equation x = (0.1 m) cos[(1.26s-1)t]. At time t = 0.8 s, what is the magnitude of the acceleration of the object?

Answer 1

The magnitude of the acceleration is 0.0847 m/s²

Step-by-step explanation:

Given:

Displacement equation for the spring:

x = 0.1*cos(1.26*t)

Acceleration is the second derivative of displacement w.r.t.

Thus,

`a=\frac {\partial^2x}{\partial t^2}`

`a=\frac {\partial^2(0.1* cos(1.26t)}{\partial t^2}`

`a=0.1* 1.26* 1.26 (-cos(1.26t))`

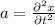
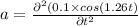
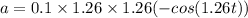
When t = 0.8 sec,

`a=-0.15876* (cos(1.26* 0.8))`

`a=-0.15876* 0.5336\ ms^(-2)`

`a=-0.0847\ ms^(-2)`

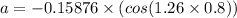
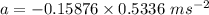
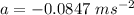
The magnitude of the acceleration is 0.0847 m/s².