Question

A block of glass with flat sides is surrounded by air. A ray of light traveling in the glass (refractive index na) is incident on the flat interface with air at the top surface of the block of glass. You observe that no light is refracted into the air if the incident ray in the glass has an angle of incidence (measured relative to the normal to the surface of the glass) greater than 40.2°. What is the refractive index of the glass?

Answer 1

Refractive index of the glass is 1.549

Step-by-step explanation:

Using the snell's law

we have

n₁sinΘ₁ = n₂sinΘ₂

where,

n₁ = refractive index of the glass

n₂ = refractive index of the air = 1

Θ₁ = Angle of incidence

Θ₂ = angle of refraction

since no light is refracted

thus,

`{n_1=}(n_2\sin\theta_2)/(\sin\theta_1)`

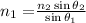
substituting the values, we get

`{n_1=}(1*\sin90^o)/(\sin40.2^o)`

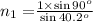
or

n₁ = 1.549