Question

The electric field strength is 4.60×104 V/m inside a parallel-plate capacitor with a 2.1 mm spacing. A proton is released from rest at the positive plate. What is the proton's speed when it reaches the negative plate? Please give answer in m/s and show all work!

Answer 1

`v=1.36* 10^5\ m/s`

Step-by-step explanation:

It is given that,

Electric field strength inside a parallel plate capacitor,
`E=4.6* 10^4\ V/m`

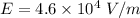
Spacing between plates, d = 2.1 mm = 0.0021 m

A proton is released from rest at the positive plate, u = 0

We need to find the speed of proton when it reaches the negative plate of the capacitor. Let it is given by v.

`qE=ma`

`a=(qE)/(m)`

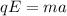
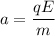
Using third equation of motion as :

`v^2-u^2=2ad`

`v^2=2ad`

`v=√(2ad)`

`v=\sqrt{2(qE)/(m){d}`

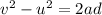
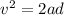
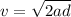
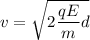
Where,

q is the charge on proton

m is the mass of the proton

`v=\sqrt{2* (1.6* 10^(-19)* 4.6* 10^4)/(1.67* 10^(-27))* {0.0021}}`

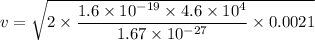
v = 136052.12 m/s

or

`v=1.36* 10^5\ m/s`

So, the speed of proton when it reaches the negative plate is
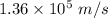`1.36* 10^5\ m/s`. Hence, this is the required solution.

Answer 2

1.36 x 10^5 m/s

Step-by-step explanation:

E = 4.6 x 10^4 V/m

d = 2.1 mm = 2.1 x 10^-3 m

The kinetic energy of proton is due to the potential difference between the plates. Let v be the speed.

1/2 mv^2 = q V

v^2 = 2 e V / m

V = E d = 4.6 x 10^4 x 2.1 x 10^-3 = 96.6 V

v^2 = (2 x 1.6 x 10^-19 x 96.6) / (1.67 x 10^-27)

v = 1.36 x 10^5 m/s