Answer:
a) Bullet will hit
b) Bullets will not hit
Step-by-step explanation:
Given:
The velocity of the bullet, u =
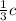 in the rest frame of the bullet pursuit car
in the rest frame of the bullet pursuit car
The velocity of the original frame of reference, v =
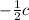 with respect to the pursuit car.
with respect to the pursuit car.
Now, according to the Galileo
the velocity of the bullet in the original frame of reference (u') will be
u' = u - v
on substituting the values we get
u' =
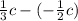
or
u' =
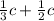
or
u' =
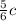
since this velocity (
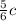 ) is greater than the (
) is greater than the (
 )
)
hence,
the bullet will hit
Now, according to the Einstein theory
the velocity of the bullet in the original frame of reference (u') will be
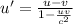
on substituting the values we get
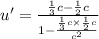
or
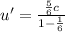
or
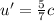
since,
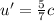 is less than (
is less than (
 ), this means that the bullet will not hit
), this means that the bullet will not hit