Question

Discuss Joule-Thompson effect with relevant examples and formulae.

Answer 1

`\mu _j=(1)/(C_p)\left [T\left((\partial v)/(\partial T)\right)_p-v\right]dp`

Step-by-step explanation:

Joule -Thompson effect

Throttling phenomenon is called Joule -Thompson effect.We know that throttling is a process in which pressure energy will convert in to thermal energy.

Generally in throttling exit pressure is low as compare to inlet pressure but exit temperature maybe more or less or maybe remains constant depending upon flow or fluid flow through passes.

Now lets take Steady flow process

Let

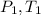`P_1,T_1` Pressure and temperature at inlet and

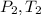`P_2,T_2` Pressure and temperature at exit

We know that Joule -Thompson coefficient given as

`\mu _j=\left((\partial T)/(\partial p)\right)_h`

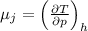
Now from T-ds equation

dh=Tds=vdp

So

`Tds=C_pdt-\left [T\left((\partial v)/(\partial T)\right)_p\right]dp`

⇒
`dh=C_pdt-\left [T\left((\partial v)/(\partial T)\right)_p-v\right]dp`

So Joule -Thompson coefficient

`\mu _j=(1)/(C_p)\left [T\left((\partial v)/(\partial T)\right)_p-v\right]dp`

This is Joule -Thompson coefficient for all gas (real or ideal gas)

We know that for Ideal gas Pv=mRT

`(\partial v)/(\partial T)=(v)/(T)`

So by putting the values in

`\mu _j=(1)/(C_p)\left [T\left((\partial v)/(\partial T)\right)_p-v\right]dp`

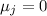`\mu _j=0` For ideal gas.