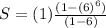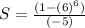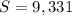Question

What is the sum of the geometric sequence-1,6,36 if there are 6 terms

Answer 1

The sum is
`9,331`

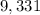
Explanation:

we have

`1,6,36,...`

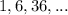
we have

`a1=1`

`a2=6`

`a3=36`

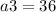
Find the common ratio r

`a2/a1=6/1=6`

`a3/a2=36/6=6`

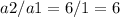
The common ratio is r=6

The formula to calculate the sum in a geometric sequence is equal to

`S=a1((1-r^(n)))/((1-r))`

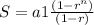
where

n is the number of terms

r is the common ratio

a1 is the first term

we have

`n=6`

`a1=1`

`r=6`

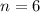
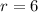
substitute

`S=(1)((1-(6)^(6)))/((1-6))`

`S=((1-(6)^(6)))/((-5))`

`S=9,331`