Question

a rescue mission to a space station at 300 nmi circular orbit starts with a launch with perigee at the surface of the earth and crosses the space station orbit with V= 9000 m/s and an elevation angle of 15 degree a) describe the trajectory b) what is the TOF to the space station orbit? how does it compare with the time of a Hohmann transfer? c) what is the required launch velocity?

Answer 1

e = 1.41 and time of flight is 11.926 and velocity is 41579.38 m/sec

Step-by-step explanation:

Give data

circular orbit r = 300 nm

V= 9000 m/s

angle = 15 degree

to find out

trajectory and TOF and required launch velocity

solution

first we use eccentricity formula i.e

e = radius × velocity² / GM

GM is standard gravitational parameter here 3.98 ×
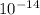`10^(-14)` -1

radius is earth radius + orbit

radius = 6.9333 ×
`10^(6)` m

put these value and calculate e

e = 6.9333 ×
`10^(6)` × 90000² / ( 3.98 ×
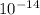`10^(-14)` -1 )

e = 1.41

here we found that e is greater than 1

now we calculate time of flight (TOF)

first we calculate the length i.e

length (semi latus) = r (1 + e cos θ )

here r = 555000 e is 1.41 and angle is 15 degree

so length = 555000 (1+ 1.41 cos 15 )

length = 1.31 ×
`10^(6)` m

so as that semi major axis will be here

major axis = length / 1 - e²

major axis = 1.31 ×
`10^(6)` / 1- 1.41²

major axis will be -1.365 ×
`10^(6)` m

and now we calculate eccentricity

cosh (F) i.e = e+cosθ / 1 + ecosθ = 1.41+cos15 / 1 + 1.41 cos15

so F will be = 1.89 ×
`10^(-3)` rad

so now TOF will be calculate

time of flight = ( e sin h f - F ) (
`√(-a^3/Gm)` )

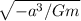time of flight = ( e sin h 0.108 - 1.89
`10^(-3)` ) (
`√((-1.356*10^3)^3/3.98*10^14)` )

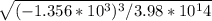so time of flight is 11.926

and last velocity will be by this given formula

velocity =
`(GM (2/r - 1/a)^(1/2)`

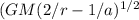
so velocity = (3.98 ×
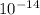`10^(-14)` (2/0.555 ×
`10^(6)` - 1 / -1.365 ×
`10^(6)` )^{1/2}

so velocity is 41579.38 m/sec