Step-by-step explanation:
1. Mass of the proton,
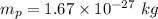
Wavelength,
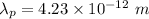
We need to find the potential difference. The relationship between potential difference and wavelength is given by :
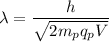
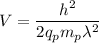
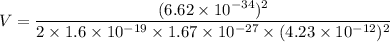
V = 45.83 volts
2. Mass of the electron,
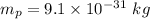
Wavelength,
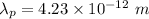
We need to find the potential difference. The relationship between potential difference and wavelength is given by :
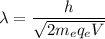
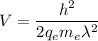
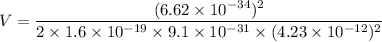
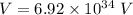
V = 84109.27 volt
Hence, this is the required solution.