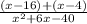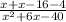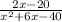Question

Which expression is equal to f(x) + g(x)?

f(x)=x-16/x^2+6x-40x fo x /= -10 and x /= 4

g(x)=1/x+10x for x /= -10


(Answer choices given in photo)

Answer 1

`(2x-20)/(x^2+6x-40)`

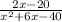
Explanation:

`f(x)+g(x)`

`(x-16)/(x^2+6x-40)+(1)/(x+10)`

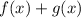
I'm going to factor that quadratic in the first fraction's denominator to figure out what I need to multiply top and bottom of the other fraction or this fraction so that I have a common denominator.

I want a common denominator so I can write as a single fraction.

So since the leading coefficient is 1, all we have to do is find two numbers that multiply to be c and at the same thing add up to be b.

c=-40

b=6

We need to find two numbers that multiply to be -40 and add to be 6.

These numbers are 10 and -4 since (10)(-4)=-40 and 10+-4=6.

So the factored form of
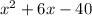`x^2+6x-40` is
`(x+10)(x-4)`.

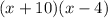So the way the bottoms will be the same is if I multiply top and bottom of my second fraction by (x-4).

This will give me the following sum so far:

`(x-16)/(x^2+6x-40)+(x-4)/(x^2+6x-40)`

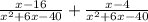
Now that the bottoms are the same we just need to add the tops and then we are truly done:

`((x-16)+(x-4))/(x^2+6x-40)`

`(x+x-16-4)/(x^2+6x-40)`

`(2x-20)/(x^2+6x-40)`