Question

The equilibrium constant, Kc, for the following reaction is 77.5 at 600 K. CO(g) + Cl2(g) COCl2(g) Calculate the equilibrium concentrations of reactant and products when 0.442 moles of CO and 0.442 moles of Cl2 are introduced into a 1.00 L vessel at 600 K. [CO] = M [Cl2] = M [COCl2] = M

Answer 1

[COCl₂] = 0.373 mol·L⁻¹

[CO] = [Cl₂] = 0.069 mol·L⁻¹

Step-by-step explanation:

The balanced equation is

CO + Cl₂ ⇌ COCl₂

Data:

Kc = 77.5

n(CO₂) = 0.442 mol

n(Cl₂) = 0.442 mol

V = 1.00 L

1. Calculate the initial concentration of CO and Cl₂

`c = \frac{\text{0.442 mol}}{\text{1.00 L}} = \text{1.00 mol/L}`

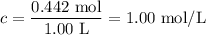
Step 2. Set up an ICE table.

`\begin{array}{ccccccc}\rm \text{CO}& + & \text{Cl$_(2)$} & \, \rightleftharpoons \, & \text{COCl$_(2)$} & & \\0.442 & & 0.442 & & 0 & & \\-x & & -x& & +x & & \\0.442-x & & 0.442 - x & & x & &\\\end{array}\\`

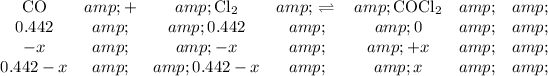
Step 3. Calculate the equilibrium concentrations

`K_{\text{c}} = \frac{\text{[COCl$_(2)$]}}{\text{[CO][Cl$_2$]}} = (x)/((0.442 - x)^(2)) = 77.5\\\begin{array}{rcl}\\(x)/((0.442 - x)^(2)) & = & 77.5\\\\x & = & 77.5(0.442 - x)^(2)\\x & = & 77.5(0.1954 - 0.884x + x^(2)\\x & = & 15.14 - 68.51x + 77.5x^(2)\\77.5x^(2) - 69.51x + 15.14 & = & 0\\x & = & \mathbf{0.373}\\\end{array}`

[COCl₂] = x mol·L⁻¹ = 0.373 mol·L⁻¹

[CO] = [Cl₂] = (0.442 - 0.373) mol·L⁻¹ = 0.069 mol·L⁻¹