First compute the probability that a bill would exceed $115. Let
 be the random variable representing the value of a monthly utility bill. Then transforming to the standard normal distribution we have
be the random variable representing the value of a monthly utility bill. Then transforming to the standard normal distribution we have

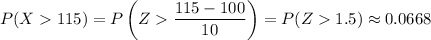
Then out of 300 randomly selected bills, one can expect about 6.68% of them to cost more than $115, or about 20.