Question

Consider a simple tension member that carries an axial load of P=22.44N. Find the total elongation in the member due to the load. Assume that the member is made of steel, which has a modulus of elasticity of E=204.00 N/mm2. Also assume that the member is 3048 mm long and has a cross-sectional area of 1290 mm2

Answer 1

The total elongation for the tension member is of 0.25mm

Step-by-step explanation:

Assuming that material is under a linear deformation then the relation between the stress and the specific elongation is given as:

`\sigma=E*\epsilon` (1)

Where E is the modulus of elasticity, σ the stress and ε the specific deformation. Also, the total longitudinal elongation can be expressed as:

`\delta L=L*\epsilon` (2)

Here L is the member extension and δL the change total longitudinal elongation.

Now if the stress is found then the deformation can be calculated by solving the stress-deformation equation (1). The stress applied sigama is computed dividing the axial load P by the cross-sectional area A:

`\sigma=P/A`

`\sigma=22.44N / 1290 mm^2`

`\sigma=0.0174 N/mm^2`

Solving for epsilon and replacing the calculated value for the stress and the value for the modulus of elasticity:

`=\sigma=E*\epsilon`

`\epsilon=\sigma/E`

`\epsilon=0.0174 (N)/(mm^2)/\ 204 (N)/(mm^2)`

`\epsilon=8.53*10^-{5}`

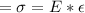
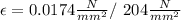
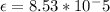
Finally introducing the specific deformation and the longitudinal extension in the equation of total elongation (2):

`\delta L=3048 mm * 8.53*10^(-5)`

`\delta L= 0.25 mm`