Question

PLEASE HELP!!!

Eliminate the parameter. x = 5 cos t, y = 5 sin t. Answer must be a rectangular equation

Answer 1

`x^2+y^2=25`

Explanation:

Recall the following Pythagorean Identity:

`\sin^2(\theta)+\cos^2(\theta)=1`

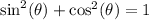
Let's solve the x equation for cos(t) and the y equation for sin(t).

After the solve we will plug into our above identity.

x=5cos(t)

Divide both sides by 5:

(x/5)=cos(t)

y=5sin(t)

Divide both sides by 5:

(y/5)=sin(t)

Now we are ready to plug into the identity:

`\sin^2(t)+\cos^2(t)=1`

`((y)/(5))^2+((x)/(5))^2=1`

`(x^2)/(5^2)+(y^2)/(5^2)=1`

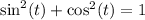
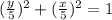
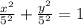
Multiply both sides by 5^2:

`x^2+y^2=5^2`

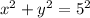
This is a circle with center (0,0) and radius 5.

All I did to get that was compare our rectangular equation we found to

`(x-h)^2+(y-k)^2=r^2`

where (h,k) is the center and r is the radius of a circle.