Answer:
1705/64
Explanation:
A geometric series contains terms that are in the form
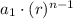 where
where
 is the first term and
is the first term and
 is common ratio.
is common ratio.
A common ratio is the number that is used to find the next term by multiplying previous term by
 .
.
Now we can use a formula and we would be using
 where n is the number of terms you are adding and
where n is the number of terms you are adding and
 is the first term and r is the common ratio.
is the first term and r is the common ratio.
Before we do that, I'm going to do this without that formula. Sum means we are just going to add these terms after finding them.
The first term is 20.
The second term is (1/4)(20)=5.
Third term is (1/4)(5)=5/4.
Fourth term is (1/4)(5/4)=5/16.
The fifth term is (1/4)(5/16)=5/64.
Now we add them (20)+(5)+(5/4)+(5/16)+(5/64)
Putting this into the calculator gives me: 1705/64.
Now let's do the formula way as well.
Again we have:
r=1/4

n=5 since we adding the first 5 terms:
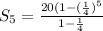
![S_5=\frac{20(1-(1)/(1024)){(3)/(4)}]()
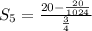
Dividing by 3/4 is the same as multiply by 4/3.
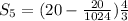
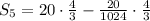


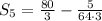

Multiplying first fraction by 64/64:
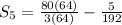

{tex]S_5=\frac{5115}{192}[/tex]
Dividing to and bottom by 3:
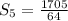 .
.