Answer:
A hole at x=-4.
Explanation:
This is a fraction so we have to worry about division by zero.
The only time we will be dividing by 0 is when x+4 is 0.
Solving the equation
x+4=0 for x:
Subtract 4 on both sides:
x=-4
So there is either a vertical asymptote or a hole at x=-4.
These are the kinds of discontinuities we can have for a rational function.
If there is a hole at x=-4, then x=-4 will make the top zero and can be cancelled out after simplification.
If is is a vertical asymptote, x=-4 will make the top NOT zero.
Let's see what -4 for x in x^2+6x+8 gives us:
(-4)^2+6(-4)+8
16+-24+8
-8+8
0
Top and bottom are 0 when x=-4.
Let's see what happens after simplication.
We are going to factor a^2+bx+c if factorable by finding two numbers that multiply to be c and add up to be b.
So what 2 numbers together multiply to be 8 and add up to be 6.
I hoped you said 4 and 2 because (4)(2)=8 where 4+2=6.
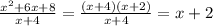
We we able to cancel out that factor that was giving us x=-4 is a zero.
Therefore there is a hole at x=-4.