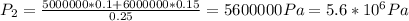Question

A tank has a volume of 0.1 m3 and is filled with He gas at a pressure of 5 x 106 Pa. A second tank has a volume of 0.15 m' and is filled with He gas at a pressure of 6 x 106 Pa. A valve connecting the two tanks is opened. Assumıng He to be a monatomic ideal gas and the walls of the tanks to be adiabatic and rigıd, find the final pressure of the system Hint: Note that the internal energy is constant.

Answer 1

`P=5.6*10^(6) Pa`

Step-by-step explanation:

Consider that, as the system is adiabatic,
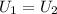`U_(1)= U_(2)` where U1 and U2 are the internal energies before the process and after that respectively.

Consider that:
`U=H-PV`, and that the internal energy of the first state is the sum of the internal energy of each tank.

So,
`H_(1)-P_(1)V_(1)=H_(2)-P_(2)V_(2)\\H_(1)^(A) -P_(1)^(A)V_(1)^(A)+H_(1)^(B) -P_(1)^(B)V_(1)^(B)=H_(2)-P_(2)V_(2)`

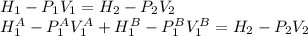
Where A y B are the tanks. The enthalpy for an ideal gas is only function of the temperature, as the internal energy is too; so it is possible to assume:
`H_(1)=H_(2)\\H_(1)^(A)+H_(1)^(B) =H_(2)`

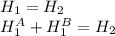
So,
`P_(1)^(A)V_(1)^(A)+P_(1)^(B)V_(1)^(B)=P_(2)V_(2)`

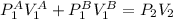
Isolating
`P_(2)`,

`P_(2)=(P_(1)^(A)V_(1)^(A)+P_(1)^(B)V_(1)^(B))/(V_(2))`

`V_(2)=V_(1)^(A)+V_(1)^(B)=0.25m^(3)`

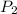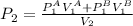
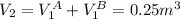
So,

`P_(2)=(5000000*0.1+6000000*0.15)/(0.25)=5600000Pa=5.6*10^(6) Pa`