Question

A rigid, sealed tank initially contains 2000 kg of water at 30 °C and atmospheric pressure. Determine: a) the volume of the tank (m3 ). Later, a pump is used to extract 100 kg of water from the tank. The water remaining in the tank eventually reaches thermal equilibrium with the surroundings at 30 °C). Determine: b) the final pressure (kPa).

Answer 1

Given:

mass of water, m = 2000 kg

temperature, T =
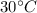`30^(\circ)C` = 303 K

extacted mass of water = 100 kg

Atmospheric pressure, P = 101.325 kPa

Solution:

a) Using Ideal gas equation:

PV = m
`\bar{R}`T (1)

where,

V = volume

m = mass of water

P = atmospheric pressure

`\bar{R} = (R)/(M)`

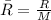
R= Rydberg's constant = 8.314 KJ/K

M = molar mass of water = 18 g/ mol

Now, using eqn (1):

`V = \frac{m\bar{R}T}{P}`

`V = (2000* (8.314)/(18)* 303)/(101.325)`

`V = 2762.44 m^(3)`

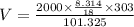
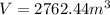
Therefore, the volume of the tank is
`V = 2762.44 m^(3)`

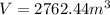
b) After extracting 100 kg of water, amount of water left, m' = m - 100

m' = 2000 - 100 = 1900 kg

The remaining water reaches thermal equilibrium with surrounding temperature at T' =
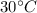`30^(\circ)C` = 303 K

At equilibrium, volume remain same

So,

P'V = m'
`\bar{R}`T'

`P' = (1900* (8.314)/(18)* 303)/(2762.44)`

Therefore, the final pressure is P' = 96.258 kPa