Question

A compressed-air drill requires an air supply of 0.25 kg/s at gauge pressure of 650 kPa at the drill. The hose from the air compressor to the drill has a 40 mm diameter and is smooth. The maximum compressor discharge gauge pressure is 690 kPa. Neglect changes in air density and any effects of hose curvature. Air leaves the compressor at 40° C. What is the longest hose that can be used?

Answer 1

L = 46.35 m

Step-by-step explanation:

GIVEN DATA

\dot m = 0.25 kg/s

D = 40 mm

P_1 = 690 kPa

P_2 = 650 kPa

T_1 = 40° = 313 K

head loss equation

`[(P_1)/(\rho) +\alpha (v_1^2)/(2) +gz_1] -[(P_2)/(\rho) +\alpha (v_2^2)/(2) +gz_2] = h_l +h_m`

where
`h_l = ( flv^2)/(2D)`

`h_m minor loss`

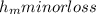
density is constant

`v_1 = v_2`

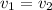
head is same so,
`z_1 = z_2`

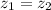
curvature is constant so
`\alpha = constant`

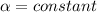
neglecting minor losses

`(P_1)/(\rho)  -(P_2)/(\rho) = ( flv^2)/(2D)`

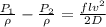
we know
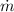`\dot m` is given as
`= \rho VA`

`\rho =(P_1)/(RT_1)`

`\rho =(690 *10^3)/(287*313) = 7.68 kg/m3`

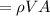
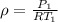
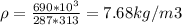
therefore

`v = (\dot m)/(\rho A)`

`V =(0.25)/(7.68 (\pi)/(4) *(40*10^(-3))^2)`

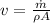
V = 25.90 m/s

`Re = (\rho VD)/(\mu)`

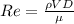
for T = 40 Degree,
`\mu = 1.91*10^(-5)`

`Re =(7.68*25.90*40*10^(-3))/(1.91*10^(-5))`

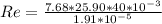
Re = 4.16*10^5 > 2300 therefore turbulent flow

for Re =4.16*10^5 , f = 0.0134

Therefore

`(P_1)/(\rho)  -(P_2)/(\rho) = ( flv^2)/(2D)`

`L = ((P_1-P_2) 2D)/(\rho f v^2)`

`L =((690-650)*`10^3* 2*40*10^(-3))/(7.68*0.0134*25.90^2)`

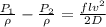
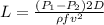
L = 46.35 m