Question

The acceleration (in m/s^2) of a linear slider (undergoing rectilinear motion) within a If the machine can be expressed in terms of its velocity (in m/s) and is given by α=1/4v^2 = if the slider starts at rest, find the time at which its velocity is 3.3 m/s.

Answer 1

47.91 sec

Step-by-step explanation:

it is given that
`\alpha =(1)/(4v^(2))`

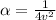
at t=0 velocity =0 ( as it is given that it is starting from rest )

we have to find time at which velocity will be 3.3
`(m)/(sec^(2))`

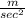
we know that
`\alpha =(dv)/(dt)=(1)/(4v^(2))`

`4v^(2)dv=dt`

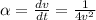
integrating both side

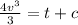`(4v^(3))/(3)=t+c`---------------eqn 1

at t=o it is given that v=0 putting these value in eqn 1 c=0

so
`(4v^(3))/(3)=t`

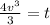
when v= 3.3
`(m)/(sec^(2))`

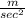
t=
`(4)/(3)* 3.3^(3)`

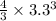
=47.91 sec