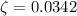Question

Consider an open loop 1-degree-of-freedom mass-spring damper system. The system has mass 4.2 kg, and spring stiffness of 85.9 N/m, and damping coefficient of 1.3 N.s/m. What is the non-dimensional damping ratio of the system? Use at least 4 significant digits after the decimal point.

Answer 1

Damping ratio
`\zeta =0.0342`

Step-by-step explanation:

Given that

m=4.2 kg,K=85.9 N/m,C=1.3 N.s/m

We need to find damping ratio

We know that critical damping co-efficient

`C_c=2\sqrt {mk}`

`C_c=2\sqrt {4.2* 85.9}`

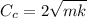
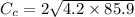
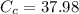`C_c=37.98` N.s/m

Damping ratio(
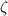`\zeta`) is the ratio of damping co-efficient to the critical damping co-efficient

So
`\zeta =(C)/(C_c)`

`\zeta =(1.3)/(37.98)`

`\zeta =0.0342`

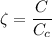
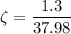
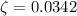
So damping ratio
`\zeta =0.0342`