Question

A plane wall of length L, constant thermal conductivity k and no thermal energy generation undergoes one-dimensional, steady-state conduction. The left hand side surface of the wall is subjected to a constant heat flux q The right hand side surface has a uniform temperature of T,. Using the standard approach, find the temperature distribution, the heat flux and rate of heat transfer.

Answer 1

Temperature distribution is
`T(x)=(q)/(k)(L-x)+T`

Heat flux=q

Heat rate=q A

Step-by-step explanation:

We know that for no heat generation and at steady state

`(\partial^2 T)/(\partial x^2)=0`

`(\partial T)/(\partial x)=a`

`T(x)=ax+b`

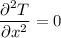
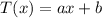
a and are the constant.

Given that heat flux=q

We know that heat flux given as

`q=-K(dT)/(dx)`

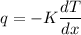
From above we can say that

`a= -(q)/(K)`

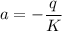
Alos given that when x= L temperature is T(L)=T

`T= -(q)/(K)L+b`

`b=T+(q)/(K)L`

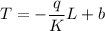
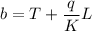
So temperature T(x)

`T(x)=-(q)/(K)x+T+(q)/(K)L`

`T(x)=(q)/(k)(L-x)+T`

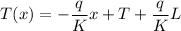
So temperature distribution is
`T(x)=(q)/(k)(L-x)+T`

Heat flux=q

Heat rate=q A (where A is the cross sectional area of wall)