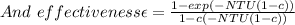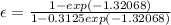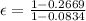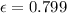Answer:Counter,
0.799,
1.921
Step-by-step explanation:
Given data

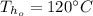
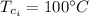

Since outlet temperature of cold liquid is greater than hot fluid outlet temperature therefore it is counter flow heat exchanger
Equating Heat exchange
![m_hc_(ph)\left [ T_(h_i)-T_(h_o)\right ]=m_cc_(pc)\left [ T_(c_o)-T_(c_i)\right ]](https://img.qammunity.org/2020/formulas/engineering/college/317g61l1i3sno80tntxq6ut1ped09aji66.png)
 =
=
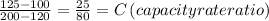
we can see that heat capacity of hot fluid is minimum
Also from energy balance
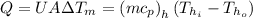
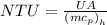 =
=
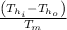
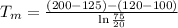
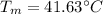
NTU=1.921