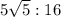Question

A scale model is 4th the size of the pump. Determine the power ratio of the pump and its scale model if the ratio of the heads is 5: 1.

Answer 1

Given:

size of scale model = 4(size of pump)

power ratio of pump and scale model = 5:1

Solution:

Let the diameter of scale model and pump be
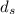`d_(s)` and
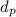`d_(p)` respectively

and head be
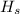`H_(s)` and
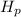`H_(p)` respectively

Now, power, P is given as a function of head(H) and dischagre(Q)

P =
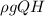`\rho gQH` (1)

From eqn (1):

`P \propto QH`

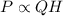
and

`QH \propto √(H)D^(2)`

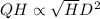
So,

`P \propto H^{(3)/(2)} D^(2)`

Therefore,

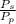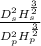
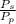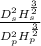
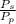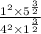
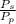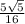
`(P_(s))/(P_(p))` =
`\frac{D_(s)^(2) H_(s)^{(3)/(2)}}{D_(p)^(2) H_(p)^{(3)/(2)}}`

`(P_(s))/(P_(p))` =
`\frac{D_(s)^(2) H_(s)^{(3)/(2)}}{D_(p)^(2) H_(p)^{(3)/(2)}}`

`(P_(s))/(P_(p))` =
`\frac{1^(2)* 5^{(3)/(2)}}{4^(2)* 1^{(3)/(2)}}`

`(P_(s))/(P_(p))` =
`(5√(5))/(16)`

`{P_(s)}:{P_(p)}` =
`{5√(5)}:{16}`