Question

Which formula can be used to describe the sequence below 27,9,3​

Answer 1

Its b on edge 2021

Explanation:

just did it

Answer 2

`a_n=27 \cdot ((1)/(3))^(n-1)`.

Explanation:

This is a geometric sequence that means there is a common ratio. That means there is a number you can multiply over and over to get the next term.

The first term is 27.

The second term is (1/3)(27)=9.

The third term is (1/3)(9)=3.

So the common ratio is 1/3.

That means you can keep multiplying by 1/3 to find the next term in the sequence.

The explicit form for a geometric sequence is
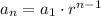`a_n=a_1 \cdot r^(n-1)` where
`a_1` is the first term and
`r` is the common ratio.

We are given
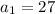`a_1=27` and
`r=(1)/(3)`.

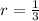So the explicit form for the given sequence is
`a_n=27 \cdot ((1)/(3))^(n-1)`.