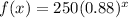Answer:
The equation which represents a population of 250 animals that decreases at an annual rate of 12% is:
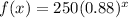
Explanation:
It is given that:
A population of 250 animals decreases at an annual rate of 12%.
This problem could be modeled with the help of a exponential function.

where a is the initial amount.
and b is the change in the population and is given by:
 if the population is decreasing at a rate r.
if the population is decreasing at a rate r.
and
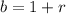 if the population is increasing at a rate r.
if the population is increasing at a rate r.
Here we have:
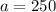
and x represents the number of year.
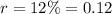
Hence, we have:
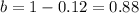
Hence, the population function f(x) is given by: