Question

Two trains travel at right angles to each other after leaving the same train station at the same time. Two hours later they are 70.46 miles apart. If one travels 9 miles per hour slower than the other, what is the rate of the faster train? (Round your answer to the nearest integer)

Answer 1

The faster train travels at a speed of 29 miles/hr

Step-by-step explanation:

Let the speed of train A be x miles/hr

So the speed of the train B is ( x - 9 ) miles/hr

After two hours, their speed will be 2x and 2( x - 9 ) respectively. and the distance between them is 70.46 miles.

So using Pythogorus theorem, we can write

`(2x)^(2)+(2x-18)^(2) = 70.46^(2)`

`8x^(2)-72x+324 = 4964.6116`

`8x^(2)-72x-4640.6116 = 0`

On solving the above equation we get

x = 29.0015 miles/hr

= 29 miles/hr

Therefore the faster train travels at a speed of 29 miles/hr

Answer 2

Speed of faster train equals 29 mph

Step-by-step explanation:

Let the speed of slower train be 'x' miles per hour and the speed of faster train be 'y' miles per hour.

Distance that slower train covers in 2 hours=
`2* x miles`

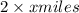
Distance that faster train covers in 2 hours=
`2* y miles`

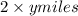
Since they move at right angles the distance between them can be found by Pythagoras formula as

`d^(2)=(2x)^(2)+(2y)^(2)\\\\d^(2)=4(x^(2)+y^(2))\\(70.46)^(2)=4(x^(2)+y^(2))\\\\\therefore (x^(2)+y^(2))=((70.46)^(2))/(4)\\\\(x^(2)+y^(2))=(4964.6)/(4)\\\\(x^(2)+y^(2))=1241.15`

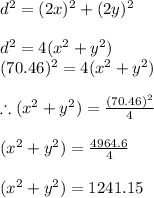
It is given that
`y=x+9`

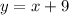
Using this in the above equation we get

`(x^(2)+y^(2))=1241.15\\\\x^(2)+(x+8)^(2)=1241.15\\2x^(2)+16x+64=1241.15\\2x^(2)+16x-1177.15=0`

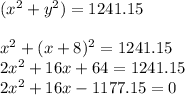
This is a quadratic equation in 'x'

Comparing with standard quadratic equation
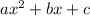`ax^(2)+bx+c` we get value of x as

`(x^(2)+y^(2))=1241.15\\\\x^(2)+(x+8)^(2)=1241.15\\2x^(2)+16x+64=1241.15\\2x^(2)+16x-1177.15=0\\\\x=\frac{-16\pm \sqrt{(16)^(2)-4* 2* -1177.15}}{2* 2}\\\\x=(-16\pm 98.35)/(4)\\\\x=20.58mph(\because speed\\eq <0)`

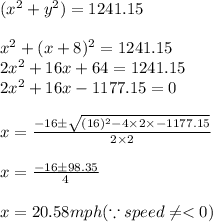
Thus speed of faster train = 28.58 mph

Speed of faster train = 19 mph