Question

Consider the functions f and g defined by \[f(x) = \sqrt{\dfrac{x+1}{x-1}}\qquad\qquad\text{and}\qquad\qquad g(x) = \dfrac{\sqrt{x+1}}{\sqrt{x-1}}.\]Explain why f and g are not the same function.

Answer 1

The given functions are not same because the domain of both functions are different.

Explanation:

The given functions are

`f(x)= \sqrt{(x+1)/(x-1)}`

`g(x) = (√(x+1))/(√(x-1))`

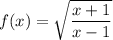
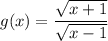
First find the domain of both functions. Radicand can not be negative.

Domain of f(x):

`(x+1)/(x-1)>0`

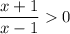
This is possible if both numerator or denominator are either positive or negative.

Case 1: Both numerator or denominator are positive.

`x+1\geq 0\Rightarrow x\geq -1`

`x-1\geq 0\Rightarrow x\geq 1`

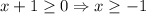
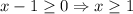
So, the function is defined for x≥1.

Case 2: Both numerator or denominator are negative.

`x+1\leq 0\Rightarrow x\leq -1`

`x-1\leq 0\Rightarrow x\leq 1`

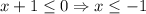
So, the function is defined for x≤-1.

From case 1 and 2 the domain of the function f(x) is (-∞,-1]∪[1,∞).

Domain of g(x):

`x+1\geq 0\Rightarrow x\geq -1`

`x-1\geq 0\Rightarrow x\geq 1`

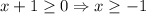
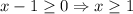
So, the function is defined for x≥1.

So, domain of g(x) is [1,∞).

Therefore, the given functions are not same because the domain of both functions are different.