Question

A boat is pulled into a dock by a rope attached to the bow of the boat and passing through a pulley on the dock that is 1 m higher than the bow of the boat. If the rope is pulled in at a rate of 1 m/s, how fast is the boat approaching the dock when it is 7 m from the dock?

Answer 1

The boat is approaching the dock when it is 7 m from the dock at a rate of 1.0102 m

Step-by-step explanation:

The situation is drawn in the image shown below.

From the image,

Applying Pythagorean theorem as:

a² + 1² = b² .....1

Differentiation both side w.r.t. time as:

`2a* (\partial a)/(\partial t)+0=2b* (\partial b)/(\partial t)`

or,

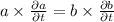`a* (\partial a)/(\partial t)=b* (\partial b)/(\partial t)`...2

Given:

The rate of the pulling of the rope in = 1 m/s

Thus,
`(\partial b)/(\partial t)=1`

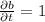
We have to find
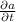`(\partial a)/(\partial t)` when a = 7 m

Using equation 1 to calculate b as:

7² + 1² = b²

b = √50 m

Using equation 2 as:

`7* (\partial a)/(\partial t)=\sqrt {50}* 1`

Thus,

`(\partial a)/(\partial t)=\frac {\sqrt {50}}{7}\ m/s=1.0102\ m/s`

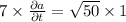
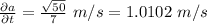
Thus, the boat is approaching the dock when it is 7 m from the dock at a rate of 1.0102 m