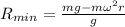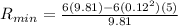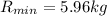Answer:
Part a)
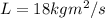
Part b)
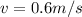
Part c)
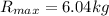
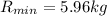
Step-by-step explanation:
As we know that Ferris wheel start from rest with angular acceleration
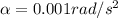
time taken = 2 min
so here we have its angular speed after t = 2min given as
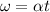
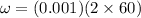

Part a)
Angular momentum of the Penguine about the center of the wheel is given as
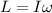
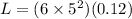
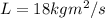
Part b)
tangential speed is given as
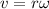
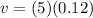
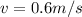
Part c)
Maximum reading of the scale at the lowest point is given as
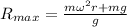
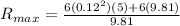
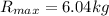
Minimum reading of the scale at the top point is given as