Question

Write an equation in siope-intercept form for a line that is (a) parallel (b) perpendicular to

the line y = 5x -- 3 and has a y-intercept of 6.

Answer 1

first off, let's notice something

`\bf y=\stackrel{\stackrel{m}{\downarrow }}{5}x-3\qquad \impliedby \begin{array} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

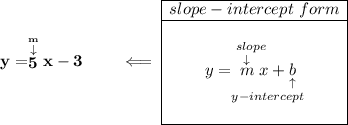
so then, any parallel line to this one will have the same slope of 5, and any perpendicular line will have a negative reciprocal of that

`\bf \stackrel{\textit{perpendicular lines have \underline{negative reciprocal} slopes}} {\stackrel{slope}{5\implies \cfrac{5}{1}}\qquad \qquad \qquad \stackrel{reciprocal}{\cfrac{1}{5}}\qquad \stackrel{negative~reciprocal}{-\cfrac{1}{5}}}`

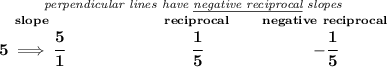
now, a y-intercept is when the graph touches the y-axis, and that happens when x = 0, so these two lines pass through the point (0, 6).

a)

parallel, slope of 5

`\bf (\stackrel{x_1}{0}~,~\stackrel{y_1}{6})~\hspace{10em} slope = m\implies 5 \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-6=5(x-0) \\\\\\ y-6=5x\implies y=5x+6`

b)

perpendicular, slope of -1/5

`\bf (\stackrel{x_1}{0}~,~\stackrel{y_1}{6})~\hspace{10em} slope = m\implies -\cfrac{1}{5} \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-6=-\cfrac{1}{5}(x-0) \\\\\\ y-6=-\cfrac{1}{5}x\implies y=-\cfrac{1}{5}x+6`