Question

The volumes of soda in quart soda bottles can be described by a Normal model with a mean of 32.3 oz and a standard deviation of 1.2 oz. What percentage of bottles can we expect to have a volume less than 32 oz?

Answer 1

Answer: We can expect about 40.13% of bottles to have a volume less than 32 oz.

Explanation:

Given : The volumes of soda in quart soda bottles can be described by a Normal model with

`\mu=\text{32.3 oz}\\\\\sigma=\text{1.2 oz}`

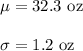
Let X be the random variable that represents the volume of a randomly selected bottle.

z-score :
`(x-\mu)/(\sigma)`

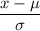
For x = 32 oz

`z=(32-32.3)/(1.2)=-0.25`

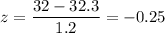
The probability of bottles have a volume less than 32 oz is given by :-

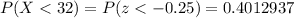`P(X<32)=P(z<-0.25)=0.4012937` [Using standard normal table]

In percent,
`0.4012937*100=40.12937\%\approx40.13\%`

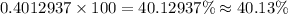
Hence, we can expect about 40.13% of bottles to have a volume less than 32 oz.