Answer:
Not a factor
Explanation:
We can use Factor Theorem to answer this question. According to this theorem, in order to find if (x - a) is a factor of a polynomial f(x), calculate f(a). If f(a) comes out to be equal to zero, this will mean that (x-a) is factor of f(x).
Here, the expression we have is (x + 7), so we need to find f(-7) in order to check if (x+7) is a factor of f(x) or not
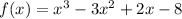
Substituting x = -7, we get:

Since f(-7) ≠ 0, (x + 7) is not a factor of the polynomial f(x)