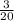Question

A bag contains 6 red marbles, 6 white marbles, and 4 blue marbles. What is the probability that someone could pull a white marble from the bag, keep it, and then pull a red marble on the second try?

Answer 1

The probability of getting white marble in the first try and red marble in the second try (without replacement) is
`(3)/(20)`

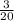
Explanation:

Given: A bag contains 6 red marbles, 6 white marbles, and 4 blue marbles.

The total numb
er of marbles in the bag = 6 + 6 + 4 = 16

Someone is pull a marble.

The probability of getting a white marble P(W)=
`(The number of favorable outcomes)/(The total number of possible outcomes)`

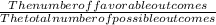
P(W) =
`(6)/(16)`

Then that marble kept it (with out replacement).

Now the total number of marbles in the bag = 6(red) + 5(white) + 4(blue) = 15

In the second try, the probability of getting a red marble P(R) =
`(6)/(15)`

These two events are dependent, because the out comes of the first event influences the outcome of the second event.

So, the probability that someone could pull a white marble from the bag, keep it, and then pull a red marble on the second try = P(W) *P(R)

=
`(6)/(16) *(6)/(15)`

Now we can multiply the fractions and simplify.

=
`(36)/(240)`

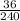
Here GCF of 36 and 240 is 12. So divide both the numerator and the denominator by 12, we get

=
`(3)/(20)`

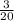
So, the probability of getting white marble in the first try and red marble in the second try (without replacement) is
`(3)/(20)`