Question

A solution is prepared by dissolving 4.66 g of KCl in enough distilled water to give 250 mL of solution. KCl is a strong electrolyte. How will the freezing point of the solution be different from that of pure water?

Answer 1

Depression in freezing point = 2 X 1.853 X 0.25 = 0.9625

Thus this will be the difference between the freezing point of pure water and the solution.

Step-by-step explanation:

On adding any non volatile solute to a solvent its boiling point increases and its freezing point decreases [these are two of the four colligative properties].

The depression in freezing point is related to molality of solution as:

ΔTf
`=iK_(f)Xmolality`

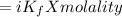
where

ΔTf= depression in freezing point

Kf= cryoscopic constant of water = 1.853 K. kg/mol.

i = Van't Hoff factor = 2 ( for KCl)

molality =
`(molesofsolute)/(massofsolvent(Kg))`

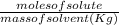
moles of solute = mass / molarmass = 4.66 / 74.55 =0.0625

mass of solvent = mass of solution (almost)

considering the density of solution to be 1g/mL

mass of solvent = 250 grams = 0.250 Kg

molality =
`(0.0625)/(0.25)= 0.25`

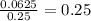
Putting values

depression in freezing point = 2 X 1.853 X 0.25 = 0.9625

Thus this will be the difference between the freezing point of pure water and the solution.

Answer 2

Answer : The solution will be
`0.931^oC` lower than water.

Explanation : Given,

Molal-freezing-point-depression constant
`(K_f)` for water =
`1.86^oC/m`

Mass of KCl (solute) = 4.66 g

Volume of water = 250 mL

Density of water = 1.00 g/mL

So,

Mass of water (solvent) =
`Density* volume=1.00g/mL* 250mL=250g=0.250kg`

Molar mass of KCl = 74.5 g/mole

Formula used :

`\Delta T_f=i* K_f* m\\\\\Delta T=i* K_f*\frac{\text{Mass of KCl}}{\text{Molar mass of KCl}* \text{Mass of water in Kg}}`

where,

`\Delta T` = change in freezing point

i = Van't Hoff factor = 2 (for KCl electrolyte)

`K_f` = freezing point constant for water =
`1.86^oC/m`

m = molality

Now put all the given values in this formula, we get

`\Delta T=2* (1.86^oC/m)* (4.66g)/(74.5g/mol* 0.250kg)`

`\Delta T=0.931^oC`

`T^o-T_s=0.931^oC`

From this we conclude that, the solution will be
`0.931^oC` lower than water.

Therefore, the solution will be
`0.931^oC` lower than water.