Question

The summer reading list for your English class has twelve books, and the list for History has eight books. You need to read three books for English and two books for History. How many different sets of books can you read?

Answer 1

Explanation:

This is a combination problem from stats. We have a total of 12 English books from which you have to 3. The order in which you pick them doesn't matter, you only need to determine how many different combinations are available to you. This is the combination formula, then:

₁₂C₃ =
`(12!)/(3!(12-3)!)`

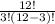
I'm just going to simplify the right side and leave off the left side til the end of the algebra because it's easier. The right side simplifies to

`(12*11*10*9!)/(3*2*1*9!)`

The 9!'s cancel each other out, leaving you with

`(12*11*10)/(3*2*1)=(1320)/(6)`

Therefore,

₁₂C₃ = 220 possible different combinations of English books from which to pick.

We'll do the same for History, which has a combination formula that looks like this:

₈C₂=
`(8!)/(2!(8-2)!)`

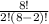
That right side expands to

`(8*7*6!)/(2*1*6!)`

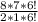
The 6!'s cancel each other out, leaving you with:

`(8*7)/(2*1)=(56)/(2)`

Therefore,

₈C₂ = 28 possible different combinations of History books from which to pick.

You may or may not need to add those together to get the answer your teacher is looking for.