Question

Help! I need help on this

Answer 1

Check the picture below.

now we simply plug all those three sides in Heron's Area Formula.

`\bf \qquad \textit{Heron's area formula} \\\\ A=√(s(s-a)(s-b)(s-c))\qquad \begin{cases} s=(a+b+c)/(2)\\[-0.5em] \hrulefill\\ a=5.8\\ b=9.75\\ c=7.39\\ s=11.47 \end{cases} \\\\\\ A=√(11.47(11.47-5.81)(11.47-9.75)(11.47-7.39)) \\\\\\ A=√(11.47(5.66)(1.72)(4.08))\implies A\approx √(455.5839955) \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ ~\hfill A\approx 21.3444~\hfill`

Answer 2

area of triangle ABC is 21.39 square units.

C is the correct option.

Explanation:

We know the formula for the area of the triangle ABC in terms of sine. The formulas are

`A=(1)/(2)ab\sin C\\\\A=(1)/(2)ac\sin B\\\\A=(1)/(2)bc\sin A`

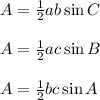
In the given triangle, we hae

b = 9.75

c = 7.39

A = 36.43°

Therefore, area of triangle ABC is given by

`A=(1)/(2)bc\sin A\\\\(1)/(2)\cdot9.75\cdot7.39\sin36.43\\\\A=21.39`

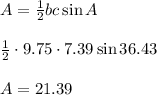
Hence, area of triangle ABC is 21.39 square units.

C is the correct option.