Question

A 15 ft ladder is sliding down a wall. The base of the ladder is sliding away from the wall at 1.5 ft/sec. How fast is the top of the ladder sliding down the wall at the instant the base of the ladder is 9 ft from the wall?

Answer 1

Answer:1.125 ft/sec

Step-by-step explanation:

Given

length of ladder =15 ft

Base of ladder is 9 m away

Angle which ladder makes with horizontal is

`cos\theta =(9)/(15)`

Let at any instant base of ladder is x m away and top of ladder is ym away from ground

therefore

`x^2+y^2=L^2`

differentiating w.r.t we get

`x\frac{\mathrm{d} x}{\mathrm{d} t}+y\frac{\mathrm{d} y}{\mathrm{d} t}=0`

`x\frac{\mathrm{d} x}{\mathrm{d} t}=-y\frac{\mathrm{d} y}{\mathrm{d} t}`

`x* \dot{x}=-y* \dot{y}`

`(x)/(y)* \dot{x}=-\dot{y}`

`\dot{y}=(3)/(4)* 1.5=(9)/(8)ft/sec`

Answer 2

The rate of ladder moving down against the wall is 1.125 ft/s

Step-by-step explanation:

Note: Refer to the attached figure

Applying the concept of the Pythagoras we have

`x^2+y^2 = H^2`

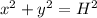
or

9²+y² = 15²

⇒y² = 225 - 81

⇒y = √144 = 12 m

also,

`x^2+y^2 = H^2`

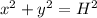
differentiating with respect to time, we get

`2x(dx)/(dt)+2y(dy)/(dt) = 0`

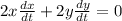
substituting the values in the above equation we get

`2* 9*frac1.5+2* 12(dy)/(dt) = 0`

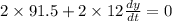
or

`27+24(dy)/(dt) = 0`

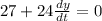
or

`(dy)/(dt) =-(27)/(24)`

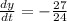
or

`(dy)/(dt) =-1.125\ ft/s`

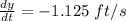
here, the negative sign depicts that the value of y is decreasing or the ladder is moving down.

hence, the rate of ladder moving down against the wall is 1.125 ft/s