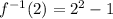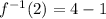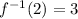Answer:
3
Explanation:
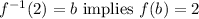
This we means to to solve the following equation for b:
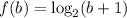
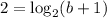 since f(b)=2
since f(b)=2
Write in equivalent exponential form:
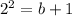
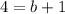
Subtract 1 on both sides:

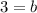
This means
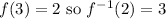
You could actually find the inverse function if you want to then replace input for the inverse with 2.
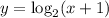
Your logarithm has base 2 and input (x+1) and output y.
The equivalent exponential form is:
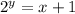
If we solve for x then at the end swap x and y we would have found the inverse function.
Let's do that:
![2^y=x+1</p><p>Subtract 1 on both sides:</p><p>[tex]2^y-1=x](https://img.qammunity.org/2020/formulas/mathematics/middle-school/p4nhptsk9pez3wa2mof2iihf9689xq6v0n.png)
Swap x and y:

The inverse function of our given function is:
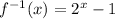
Now we need to replace x with 2: