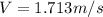Answer:
a)
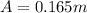
b) 29
c)
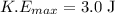
d)
Step-by-step explanation:
mass, m =0.96 g
k = 220 N/m
Total energy, E = 3.0 J
Now,
a)
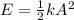
where, A is the amplitude
on substituting the values, we get
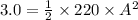
or
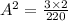
or
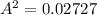
or
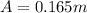
b) Time period (T) is given as:
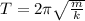
on substituting the values,we get
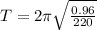
or
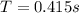
thus, number of oscillations (N) in 12s will be
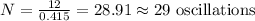
c)Maximum K.E = total mechanical energy
thus,
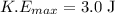
d)The angular frequency (ω) is given as:
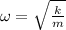
on substituting the values,we get
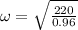
or
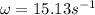
Now, the speed (V) in SHM is calculated as;
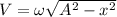
for x = 0.12m
we get
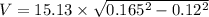
or