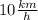Answer:
The speed on boat in still water is
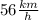 and the rate of the current is
and the rate of the current is
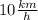
Step-by-step explanation:
Since speed ,
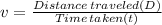
Therefore speed of motor boat while traveling upstream is
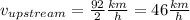
and speed of motor boat while traveling downstream is
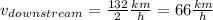
Let speed of boat in still water be
 and rate of current be
and rate of current be

Therefore
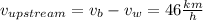 ----(A)
----(A)
and
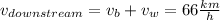 ------(B)
------(B)
Adding equation (A) and (B) we get

=>
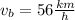 ------(C)
------(C)
Substituting the value of
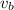 in equation (A) we get
in equation (A) we get

Thus the speed on boat in still water is
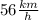 and the rate of the current is
and the rate of the current is