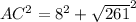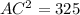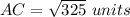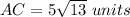Answer:
The shortest distance from A to C is
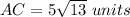
Explanation:
see the attached figure to better understand the problem
we know that
The shortest distance from A to C is the hypotenuse of the right triangle AYC
Applying the Pythagoras Theorem
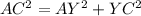
step 1
Find the length YC (hypotenuse of the right triangle YBC)
Applying the Pythagoras Theorem
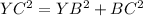
substitute the given values
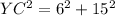
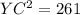

step 2
Find the shortest distance from A to C
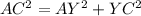
substitute the given values