Question

A silver sphere with radius 1.3611 cm at 23.0°C must slip through a brass ring that has an internal radius of 1.3590 cm at the same temperature. To what temperature must the ring be heated so that the sphere, still at 23.0°C, can just slip through?

Answer 1

The temperature must the ring be heated so that the sphere can just slip through is 106.165 °C.

Step-by-step explanation:

For brass:

Radius = 1.3590 cm

Initial temperature = 23.0 °C

The sphere of radius 1.3611 cm must have to slip through the brass. Thus, on heating the brass must have to attain radius of 1.3611 cm

So,

Δ r = 1.3611 cm - 1.3590 cm = 0.0021 cm

The linear thermal expansion coefficient of a metal is the ratio of the change in the length per 1 degree temperature to its length.

Thermal expansion for brass = 19×10⁻⁶ °C⁻¹

Thus,

`\alpha=\frac {\Delta r}{r* \Delta T}`

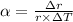
Also,

`\Delta T=T_(final)-T_(Initial)`

So,

`19* 10^(-6)=\frac {0.0021}{1.3290* (T_(final)-23.0)}`

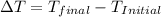
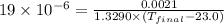
Solving for final temperature as:

`(T_(final)-23.0)=\frac {0.0021}{1.3290* 9* 10^(-6)}`

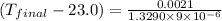
Final temperature = 106.165 °C