Question

If five numbers are selected at random from the set {1,2,3,...,20}, what is the probability that their minimum is larger than 5? (A number can be chosen more than once, and the order in which you select the numbers matters)

Answer 1

the probability that their minimum is larger than 5 is 0.2373

Explanation:

For calculate the probability we need to make a división between the total ways to selected the 5 numbers and the ways to select the five numbers in which every number is larger than 5.

So the number of possibilities to select 5 numbers from 20 is:

20 * 20 * 20 * 20 * 20

First number 2nd number 3rd number 4th number 5th number

Taking into account that a number can be chosen more than once, and the order in which you select the numbers matters, for every position we have 20 options so, there are
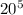`20^(5)` ways to select 5 numbers.

Then the number of possibilities in which their minimum number is larger than 5 is calculate as:

15 * 15 * 15 * 15 * 15

First number 2nd number 3rd number 4th number 5th number

This time for every option we can choose number from 6 to 20, so we have 15 numbers for every option and the total ways that satisfy the condition are
`15^(5)`

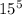
So the probability P can be calculate as:

`P=(15^(5) )/(20^(5) ) \\P=0.2373`

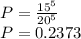
Then the probability that their minimum is larger than 5 is 0.2373