Answer:
The value of P(S or T) is 3/4.
Explanation:
It is given that S and T are mutually exclusive events. It means intersection of S and T is 0.
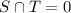
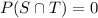
We need to find the value of P(S or T). It means we have to find the probability of union of S and T.

Substitute the given values in the above formula.
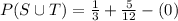

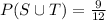
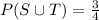
Therefore the value of P(S or T) is 3/4.